The current version of Haul Infinity uses standard straight-line segments to display roads. In future, we’re looking to transition to rendering smooth roads. The benefits of this approach include: more accurate distance calculations, and the capability to calculate and visualize road curvature for use in applying speed limits.

The following two images show a classic switchback, rendered in Haul Infinity with straight lines and Bezier splines, respectively:

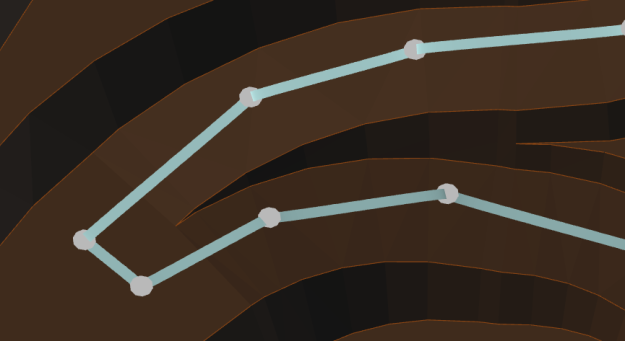
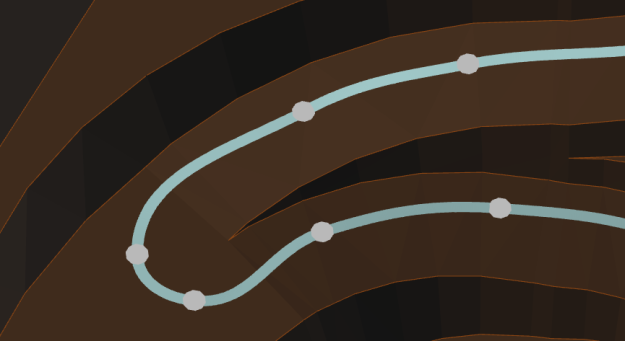
I retrieved the equations for the cubic Bezier spline from the Adobe PostScript language reference.

From page 565, the parametric form of the equation is:

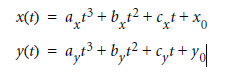
Given p0 (segment start), p3 (segment end), p1 (start anchor) and p2 (end anchor), to calculate the coefficients for the parametric form:

public Bezier(Point p0, Point p1, Point p2, Point p3) {
    _cx = 3*(p1.X - p0.X);
    _bx = 3*(p2.X - p1.X) - _cx;
    _ax = p3.X - p0.X - _cx - _bx;

    _cy = 3*(p1.Y - p0.Y);
    _by = 3*(p2.Y - p1.Y) - _cy;
    _ay = p3.Y - p0.Y - _cy - _by;

    _x0 = p0.X;
    _y0 = p0.Y;
}

Then for each subdivision of the segment (more subdivisions for more detail):

public Point Get(double t)
{
    if(t < 0.0 || t > 1.0)
        throw new InvalidOperationException();

    var t2 = t*t;
    var t3 = t2*t;

    return new Point( _ax * t3 + _bx * t2 + _cx * t + _x0, _ay * t3 + _by * t2 + _cy * t + _y0 ,_z0 + _zd*t);
}

Choosing the anchor points is up to you — some design packages require the user to specify anchor points for each road segment. To keep our software easy to use, I chose to automatically generate anchor points to create predictably smooth roads (note this code ignores the z-axis, since we need to keep user-specified grades):

public static Point CalculateHandle(Point pAttached, Point pShared, Point pOther)
{

    double axd = (pAttached.X - pShared.X);
    double ayd = (pAttached.Y - pShared.Y);

    double bxd = (pOther.X - pShared.X);
    double byd = (pOther.Y - pShared.Y);

    double at = Math.Atan2(ayd, axd);
    double at2 = Math.Atan2(byd, bxd);

    double angle = at2 - at;

    double tangentAngle = at + (angle+ Math.PI) / 2;
    double tt = Math.Tan(tangentAngle);
    double weight2 = 0.15*(bxd*bxd+byd*byd);

    double x = Math.Sqrt(weight2/(Math.Pow(tt, 2) + 1));
    double y = x*tt;

    if (Math.Abs(Math.Atan2(y, x) - at2) > Math.PI/2)
    {
        x = -x;
        y = -y;
    }

    return new Point(pShared.X + x, pShared.Y + y, 0);
}

The geometric basis for the above code is (badly) diagrammed here:

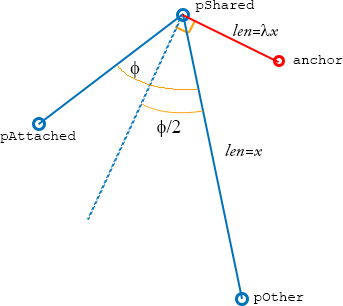
In the given code, lambda is set to Sqrt(0.15) .. but this could be adjusted to achieve desired ‘curviness’.